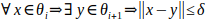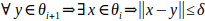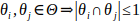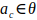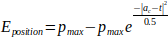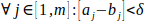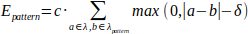CaverDock

CaverDock is based on the stepwise trajectory of the ligand along the tunnel. The tunnel geometry, approximated by a sequence of spheres, is used as an input. This sequence of spheres is obtained from tools providing the PDB file of the tunnel represented by spheres, such as Caver, for whose output file format CaverDock was optimized. The sequence of spheres is then discretized into a sequence of discs (cross-section slices of a maximal thickness set by the user). The selected ligand’s atom is positioned at the disc by a position restraint. Here the default is the atom closest to the center of mass. CaverDock then minimizes the ligand conformation and evaluates its binding free energy by using the scoring function from AutoDock Vina. The ligand trajectory is produced by all the docked poses of the ligand at each disc along the tunnel. There are however two types of trajectories, continuous and non-continuous. This non-continuous (or lower-bound) trajectory is used to estimate the lowest energy profile of the ligand’s transport through the tunnel. The actual energy may be higher since the noncontinuous movement can avoid small bottlenecks by dramatic changes in the orientation of the ligand. Finally, the pattern constraint is used to compute the continuous (upper-bound) trajectory. In each step, the ligand is docked in the vicinity of its previous position allowing only small changes in the ligand conformation. The number of possible continuous trajectories grows exponentially with the number of discs, because each transition to a new disc may lead to changes in the ligand’s position, orientation and conformation. Therefore, a heuristic method is employed to search for a continuous trajectory. When the binding free energy of a given docked conformation is significantly higher than the binding free energy of the conformation obtained from the lower-bound trajectory, backtracking is turned on. The ligand conformation is changed, and the ligand is moved successively backward to previous discs. The backtracking ends when the forward and backward trajectories converge. The backtracking will also stop if the starting disc is reached. As there is no guarantee that the resulting continuous trajectory is optimal, we call it the upper-bound trajectory as the actual energy may be lower than the computed energy. The information from the lower bound is sufficient for comparison purposes but its main limitation is that it can miss small bottlenecks. On one hand the sudden changes in orientation could potentially mimic the natural flexibility of the protein and lower the unnatural energy barriers caused by the receptor rigidity during binding or unbinding. On the other hand, the upper-bound trajectory is completely smooth, continuous. It can create unrealistic conformations in very tight parts of the tunnel, which will be apparent by sudden sharp peaks in the binding energy profile.

CaverDock computation consists of three essential steps: (i) tunnel discretization, (ii) definition of restraints, and (iii) computation of lower-bound and upper-bound trajectories.

I. Tunnel discretization

The input tunnel is represented by a set of spheres , obtained from CAVER 3.02 or a similar tool. To be further processed by CaverDock, the set of spheres is discretized into a set of discs. A disc is defined as θ = (A, u, r), where A ∈ R³ is a centre, u ∈ R³ is a normal and r > 0 is a radius. Let be a sequence of discs cutting tunnel T.

During docking with position restraint, the selected atom of a ligand is placed to consecutive discs. We need to sample the tunnel finely and also generate a continuous trajectory. Therefore, we need to upper-bound the distance between the discs, so the disc cannot force ligand to change its position too much. Let δ be the highest distance of the discs allowed and θ_i, θ_i+1 ∈ Θ. Then we require:

Moreover, we require the cuts not to intersect each other in more than a single point:

II. Definition of restraints

We used the docking implemented in AutoDock Vina and extended it with restraints. During the docking, the position of a protein-ligand complex is minimized. Let the binding energy of the protein-ligand complex computed with AutoDock Vina be E_vina. The restraints are implemented as the new energy E_position and E_pattern. The original AutoDock Vina is modified in the way that a sum E_vina + E_position + E_pattern is minimized, so the ligand finds a position, where binding-free energy is minimized in a space restricted by restraints. However, the output energy presented by CaverDock is only E_vina, so the restraints energy keeps the ligand within the defined position but does not influence the numerical value of the energy output. The ligand conformation λ is defined by the Cartesian position of its atoms: . The position restraint snaps atom a_c ∈ λ to any position at disc θ:

To keep the ligand at the disc, the restraint energy E_position is computed as follows:

where p_max is the maximum penalization energy and for t ∈ θ holds ∀u ∈ θ, u ≠ t,
|a_c − u| > |a_c − t| (i. e. t is the point in θ, which is the nearest to a_c). The bell-shaped function is used to compute E_position to avoid a too strong penalization of small distances between a_c and θ, which keeps the good numerical stability of the AutoDock Vina’s optimization method. The pattern restraint keeps the ligand λ in the vicinity of the pattern position λ_pattern:

where a_j ∈ λ, b_j ∈ λ_pattern.

The energy of the pattern restraint is computed as:

where c is a constant determining the strength of the pattern (it has been empirically set to 40). Apparently, Eq. 6 is not differentiable in the area where |a − b| = δ. We define the derivative at these points to be 0. This simple definition of pattern energy keeps the computation of the pattern restraint computationally efficient and the gradient-based optimization in Vina possible. During the minimization of E_vina + E_position + E_pattern, some restraint can be broken when the binding-free energy E_vina is too high. The restraint is considered broken when its energy is higher than 5 kcal/mol and 8 kcal/mol for the position and pattern restraint, respectively. CaverDock does not use the results in such a case.

III. Trajectory search

The lower-bound trajectory is determined by docking a ligand at each disc θ ∈ Θ, using only the position restraint. Computation of the upper-bound trajectory is more difficult. It is obtained by iterative docking onto consequent discs with restricted changes in the position of all atoms by a pattern restraint. However, such a trajectory may be sub-optimal. The ligand movement prefers the transition where the ligand follows the strongest energy gradient locally between the following steps. It may be more preferable for the ligand to make a transition to some different conformation, which may allow it to pass the energy barrier with lower energy. Therefore, CaverDock needs to search for multiple variants of ligand trajectories. We implemented a simple heuristic. The ligand is moved in one direction in the tunnel, e.g. from the binding site to the protein surface, producing a trajectory λ₁, λ₂, . . . When the binding free energy at some disc θ_i is significantly higher than the binding free energy of some known conformation λ_low at the same disc (λ_low may be obtained during lower-bound trajectory computation), we set λ_i = λ_low, and search the trajectory moving the ligand backwards to previous disks θ_i−1, θ_i−2, . . . The backtracking ends when the forward and backward trajectories converge or when the beginning of the tunnel is reached. Note that the resulting trajectory still follows one direction only. When the backtracking is used the trajectory is reversed and integrated into a forward trajectory.